From Data to Insight: Building Smarter Recovery Functions in Health Insurance with Machine Learning

Introduction
In health insurance, accurately modelling the recovery function[1] is crucial for both reserving and pricing. In Sweden, many insurers continue to rely on the recovery function developed by Insurance Sweden, last updated in 2017. The companies that calculate their own recovery function usually rely on the same methods as Insurance Sweden: using Kaplan-Meier or Nelson-Aalen estimators followed by curve fitting, typically using least squares estimation.
These traditional methods often require simplifying assumptions. The complexity of recovery functions means that models with many parameters are difficult to fit and maintain. Consequently, insurers tend to decrease the number of input features considered – often reducing them to age and gender, or just age in cases where gender is not allowed as a feature due to discriminatory regulations.
The Challenge of Modelling Long-Term Sick Leave
A recent report by the Swedish Social Insurance Agency highlights a growing challenge: long-term sick leave is on the rise across the Nordic region[2]. Norway, in particular, now exceeds the European average. Below graphs from the report show a comparison of long-term sick leave between European countries.
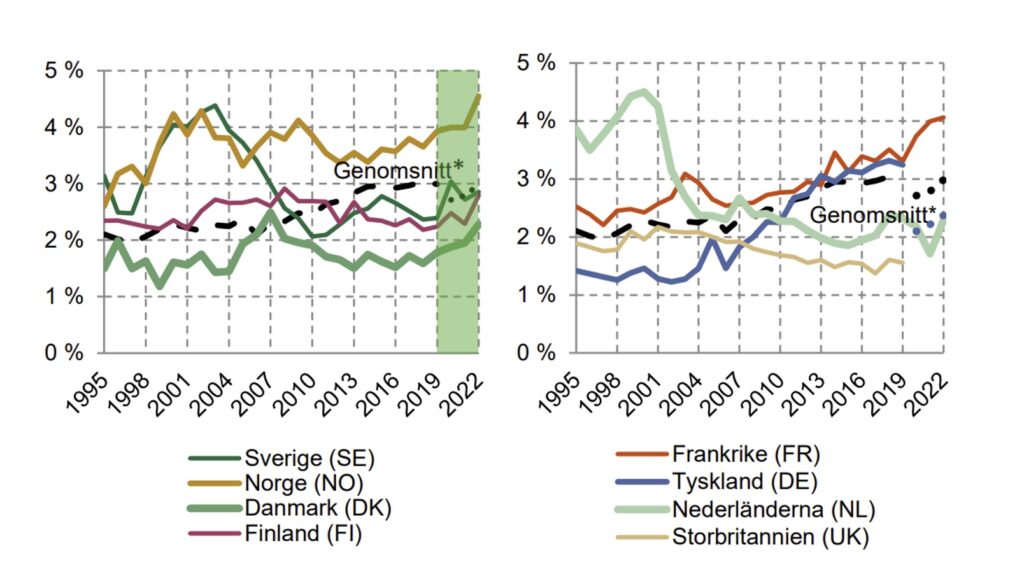
Understanding this trend is vital not just for insurers and actuaries, but also for employers and society. Better insight into what drives prolonged sick leave enables improved prediction, pricing, reserving and potentially, preventive intervention. It is, however, also important both for insurers, employers, and society as a whole to understand this in order to take the right preventive measures to decrease long-term sick leave.
From an actuarial perspective, using richer features in recovery modelling can help identify e.g. which diagnoses or conditions are associated with slower recovery. Here it is important to distinguish recovery models from those predicting the onset of illness: while onset functions estimate the likelihood of an individual becoming ill, recovery functions describe the duration of the illness. Since these processes may require different predictive features, complementing the recovery function with an adequate onset function is crucial.
Include More Predictive Features?
With modern modelling techniques, it is possible to include a broader and more informative feature set. This improves predictive power and may reduce reliance on protected characteristics such as gender – in cases where gender might act as a proxy for other features (salary or profession for example).
Here, it is important to address the different restrictions for pricing and reserving. According to a judgement from the European Court of Justice, price differentiation based on gender is not allowed (please see previous article for a deep dive in non-discriminatory pricing). However, reserving allows for differentiating between all types of features that are contributing to the risk for the insurer – as long as they are “individually responsible, reliable and objective”[3].
A Machine Learning Approach to Recovery Modelling
Machine Learning (ML)[4] provides tools that can handle many input features while uncovering complex relationships that traditional methods may miss. Techniques such as:
- Artificial Neural Networks (ANN)
- Support Vector Machines (SVM)
- Gradient Boosting Machines (GBM)
can significantly enhance recovery modelling.
However, these methods can be resource-intensive in training and difficult to interpret.
Gaussian Process Regression
Gaussian Process Regression (GPR) offers an attractive alternative. GPR is a non-parametric, Bayesian approach to regression that is often more interpretable than many machine learning models such as neural networks or ensemble methods[5].
As with many ML models, GPR does not assume a fixed functional form. Instead, it infers the function directly from the data, offering flexibility – especially useful in modelling complex phenomena like recovery.
GPR treats the function as a prior distribution over possible functions and uses observed data to infer a posterior distribution. The result is a mean function (the best estimate) and a variance function (representing uncertainty). This inherent uncertainty measure is particularly useful in pricing and reserving, where confidence intervals matter.
A basic example is shown below:
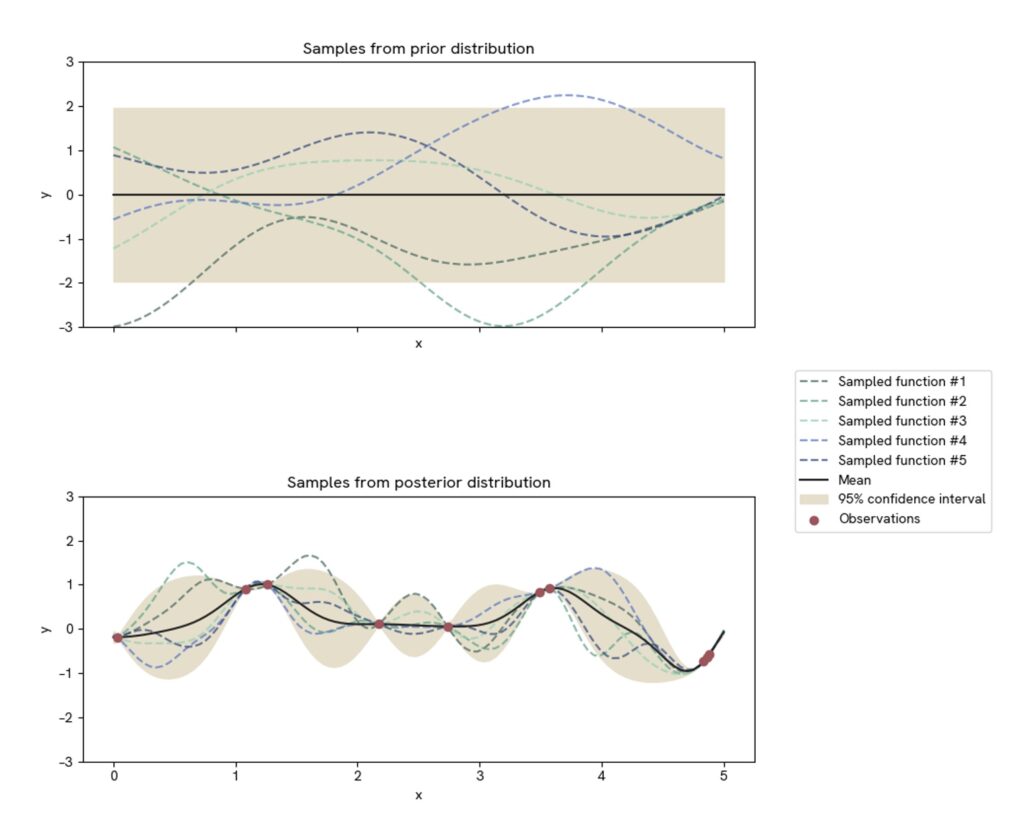
The mean function of the posterior distribution is our sought function. Note that – in each point – we are also given an estimate of the uncertainty of the prediction. This can be helpful in order not to draw too strict conclusions where there is a lack of data.
Below is an example recovery function based on insurance data from the Society of Actuaries. The features included in this model are:
- Age
- Gender
- Diagnosis
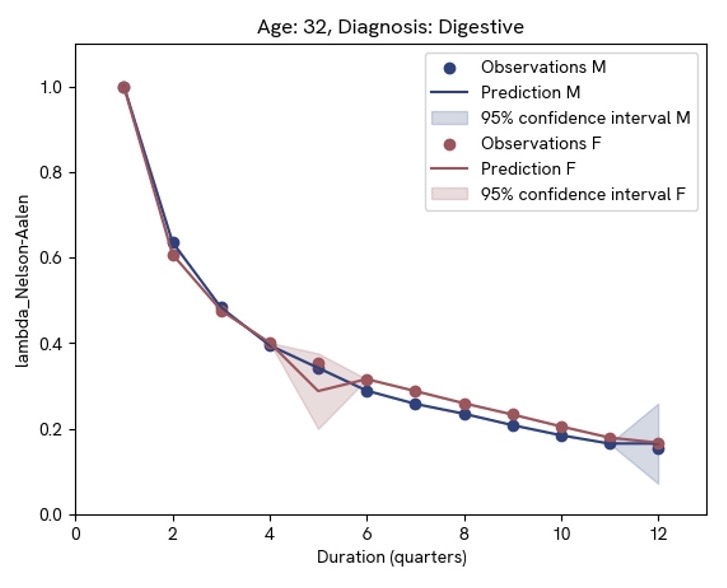
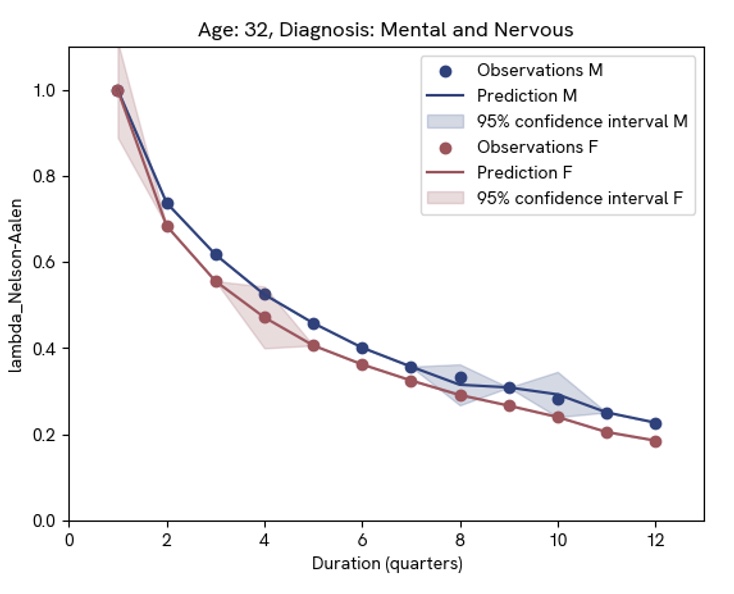
The pictures show recovery for 32-year-olds with digestive vs. mental and nervous illnesses. There is a clear difference between the two diagnoses – a difference that would be lost in a model using only age and gender as predictive features. However, the difference in gender is very small, indicating that this discriminatory feature could perhaps be omitted. Note that this reflects recovery and not onset. The onset function for different diagnoses could very well be dependent on gender; however, the recovery rate seems to be gender independent in this case.
Addressing Regulatory and Ethical Considerations
When using ML models for actuarial calculations, it is of course important to take precautions. According to the AI Act – where AI models for pricing and underwriting in health insurance are considered high-risk – insurers using these types of models must adhere to strict requirements on data quality, fairness, transparency, and human oversight. Some ML models (such as neural networks) are referred to as black box models, meaning that they are not easily interpretable. The predictions can be perfectly accurate; however, understanding why this prediction was made can be challenging. This lack of transparency is of course troubling, especially considering the AI Act (and other regulations such as GDPR and IDD). A way to address this is to use techniques called Explainable AI (or XAI). Examples include feature importance methods such as:
- Local Interpretable Model-agnostic Explanations (LIME)
- SHapley Additive exPlanations (SHAP)
- visualization techniques such as Partial Dependency Plots (PDP)
- rules extraction.
Using one or more of these methods can help interpret ML models; thus, increasing their transparency. Compared to ML models such as neural networks, GPR offers a more interpretable structure and includes built-in uncertainty estimates – a major advantage in pricing, reserving and validation.
There can of course be some challenges regarding which features are used in the model. Apart from directly discriminatory features there might be other types of information that are sensitive to collect, or act as proxy for features that might be discriminatory or linked to sensitive information (e.g. address acting as proxy for socio-economic status). This data must be collected and stored in line with e.g. GDPR regulations. It is therefore important, when training the model, to take into consideration which features are used.
Conclusion and Future Directions
Long-term sick leave is rising, creating financial and societal costs. Insurers must adopt more sophisticated tools to model these trends. Including more and/or other features than age and gender can help make better conclusions and calculations in both reserving and pricing. GPR and other ML models provide simple and powerful ways of building a multidimensional model describing recovery and other complex mathematical functions.
Beyond improving reserving accuracy, these models can also support strategic preventive efforts. By identifying which diagnoses lead to long recovery periods, insurers can prioritize early intervention or preventive care – maximizing both cost savings and social benefit.
The integration of recovery and onset modelling presents a powerful opportunity. Building a complementary onset function using similar techniques would enable even stronger predictions and pricing precision.
One key advantage of GPR is its built-in uncertainty measure. This can be leveraged for model validation, benchmarking existing reserving models, and informing the size of risk margins.
How Advisense Can Help
At Advisense, we have the ability to help health insurers improve pricing and reserving e.g. by implementing advanced ML models like GPR. We can provide tailored Proof of Concept (POC) solutions that demonstrate the power of our approach in creating accurate, multidimensional recovery functions using key features like diagnosis. The solutions ensure regulatory compliance with the AI Act and GDPR, while maintaining transparency through Explainable AI.
Let us help you take the first step towards smarter, data-driven decision-making.


Appendix – Gaussian Process Regression
[1] Swedish: avvecklingsfunktion
[2] Data for Iceland is missing.
[3] FRL 5 kap, 4 §
[4] A Machine Learning model is an algorithm that finds patterns in data. By feeding data to the model in the training process, the ML model can “learn” from it and improve predictions on new, unseen data. ML models with labelled data, i.e. input-output pairs of observations, provides for a supervised ML model.
[5] Ensemble methods in machine learning refer to techniques that combine multiple models to improve predictive performance.

