Discrimination-free pricing in non-life insurance
Price discrimination in insurance is a sensitive topic, and while it is important for insurers to differentiate their prices based on risk profiles, they must do so in a way that is legal, ethical, and non-discriminatory. The use of complex algorithms and technologies, such as AI, can increase the risk of bias and discriminatory practices. As such, insurers must ensure that their pricing models avoid not only direct but also indirect discrimination.
In this article, we explore the concept of indirect discrimination in insurance pricing, how it can occur, and how it can be handled to promote fair treatment of customers and prevent unlawful practices.

Introduction
In a recent statement on differential pricing practices EIOPA pointed out that the Insurance Distribution Directive (IDD) and the Product Oversight and Governance (POG) requirements provide a regulatory framework covering the use of differential pricing and clarifies the supervisory expectations of these frameworks. EIOPA also promotes a uniform approach amongst competent authorities in the supervision of POG, fair treatment of customers and disclosure requirements, to prevent unfair differential pricing practices that lead to customer detriment, whilst not interfering directly with business decisions on pricing.
In our previous article focusing on the regulatory issue surrounding price walking and discriminatory pricing, we address the connection between price walking and IDD in more detail.
EIOPA also emphasizes that given the increasing use of behavioral data not related to underwriting risks or costs of service companies need to ensure that the datasets used in differential pricing practices are free of bias. Processing data with complex algorithms and technologies (e.g., use of AI) may increase the risk of correlation between biased datasets and protected characteristics, which in turn increases the risk of unlawful discrimination.
In addition to price walking, there are also other forms of price discrimination which companies need to be aware of, such as situations where protected information can be inferred from correlated non-protected information. For this reason, future pricing would under POG likely need to a greater extent consider protected policyholder characteristics that are not allowed to be used for insurance pricing, to not have pricing that results in indirect discrimination by proxy.
What is price discrimination and what does it mean in an insurance context?
In Economics, price discrimination or price differentiation is the practice of charging different customers different prices for the same product based on differences in individual risk profiles. In insurance, differentiating the price depending on the underlying characteristics of the customer and/or the insured object is a key area for insurance companies to be able to offer insurance to different customers and to run a healthy business. However, insurance companies must be aware of which characteristics they use in their pricing so that the pricing meets legal and regulatory requirements.
In this article, price discrimination refers to pricing that differentiates between policyholders based on legally prohibited characteristics. Discriminatory characteristics, in this context, refers to legal and regulatory requirements that prohibit insurers from using certain characteristics in their pricing. Examples of typical discriminatory characteristics could for example be the gender or ethnicity of the policyholder. The use of protected characteristics constitutes illegal discrimination, necessitating the avoidance of such characteristics in insurance pricing models. Thus, insurers are only allowed to use non-discriminatory characteristics in their pricing. For example in the context of home insurance, the size of an apartment or whether the apartment is rented or owned are examples of typical non-discriminatory characteristics.

There are different views around the world what is regarded as discriminatory or not in a legal or regulatory context. Our scope for this article will mostly focus on the legal and regulatory requirements in the EU, but the concepts can be applied independent of the legal or regulatory framework. In addition, it is important to make a distinction between direct and indirect discrimination.
The use of prohibited characteristics as rating factors in a pricing model is an example of direct discrimination. This would mean e.g., explicitly including gender, which is illegal to include in pricing in the EU, as a rating factor in a pricing model.
Indirect discrimination is more difficult to address because it is the result of two different effects:
- Correlation between protected characteristics and other legitimately used policyholder characteristics.
- Correlation between protected characteristics and the resulting insurance prices.
Income or salary is often correlated with gender, where men in average often earn more than women, and including this as a rating factor in a pricing model will therefore act as a proxy for gender. As a result, including this rating factor may result in what is referred to as indirect discrimination.
If no discriminatory characteristics are used as rating factors, we can say that a pricing model avoids direct discrimination. Further, if a pricing model not only avoids direct discrimination, but in addition uses non-discriminatory characteristics such that one cannot make inference about discriminatory ones, the pricing model also avoids indirect discrimination. Insurance companies usually have no problem avoiding direct discrimination in their pricing, since it only means to not include such illegal characteristics in their pricing models. However, avoiding indirect discrimination in the pricing is not as easy since it means that the pricing must be adapted so that variables in the pricing model do not act as proxies for discriminatory characteristics. This is a problem for insurers since most traditionally applied pricing methods today do not consider indirect discrimination. This is a problem that has been addressed in the actuarial community recently, and in this article we will explain a method suggested by Lindholm et. al. (2022)[1] that ensures pricing models avoid indirect discrimination, while still including potential variables that act as proxies for discriminatory characteristics, and that is readily available for insurers to apply.
Why can indirect discrimination occur and how can it be handled in a pricing context?
Why can indirect discrimination occur in pricing?
As discussed in the earlier sections, insurers avoid direct discrimination by simply not using the discriminatory variables – such as gender – in their pricing models. However, as the models get increasingly complex, it is likely that they contain variables which are correlated with discriminatory variables. In other words, the prices are determined by variables, which can allow implicit inference of discriminatory features of the policyholders. This is illustrated in Figure 1.
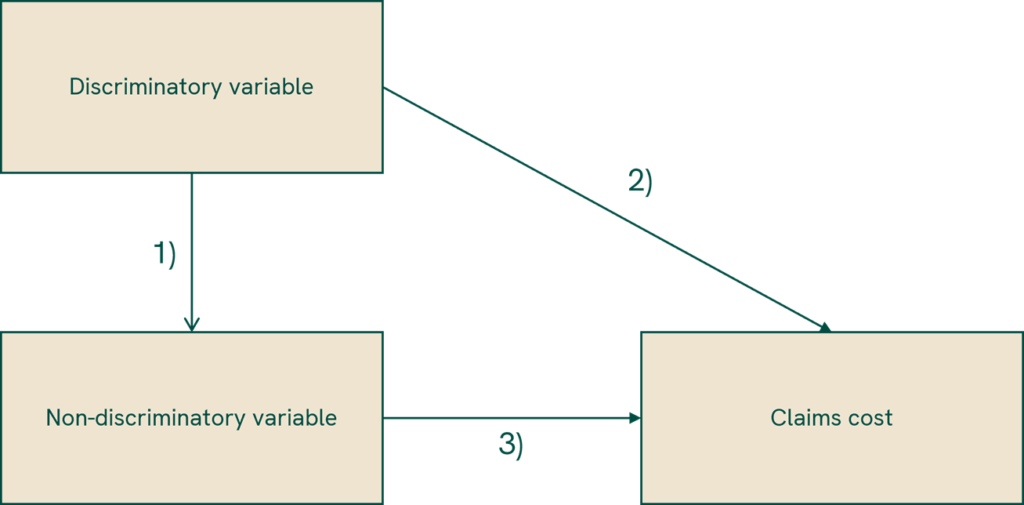
The arrows in Figure 1 have following interpretations:
- Arrow 1) represents a situation where a non-discriminatory variable is impacted by a discriminatory variable.
- In the same sense, arrow 2) represents a situation where claims cost depends on discriminatory variable.
- Finally, arrow 3) represents a situation where claims cost depends on non-discriminatory variable.
In situations like the one described above, ignoring the discriminatory variables removes the impact of arrow 2), but the impact of arrow 1) is still implicitly included in the prices.
How to handle this?
The idea of discrimination-free (in this context, discriminatory-free means avoiding both direct and indirect discrimination) is to eliminate the explanatory power that the non-discriminatory variables have for the discriminatory variables.
In appendix we present summary of a rigorous mathematical formulation of the discrimination-free price by Lindholm et al (2022), which on a high-level, the process is following:
- Identify the discriminatory variables.
- Develop models to estimate best-estimate prices, that is, estimates of the claim costs using all the available information.
- Derive the discrimination-free prices from the best-estimate prices.
These prices are presented in Figure 2 for a simulated home insurance portfolio. In addition, an unawareness price, a price which corresponds to the methodology many insurers are currently applying, that is, removing the discriminatory variable from the models, is presented.
In the example portfolio, rented apartments are riskier than owned apartments, and women possess greater risk than men. It should be noted that these characteristics in this context are purely illustrative and might not reflect real-world phenomena.
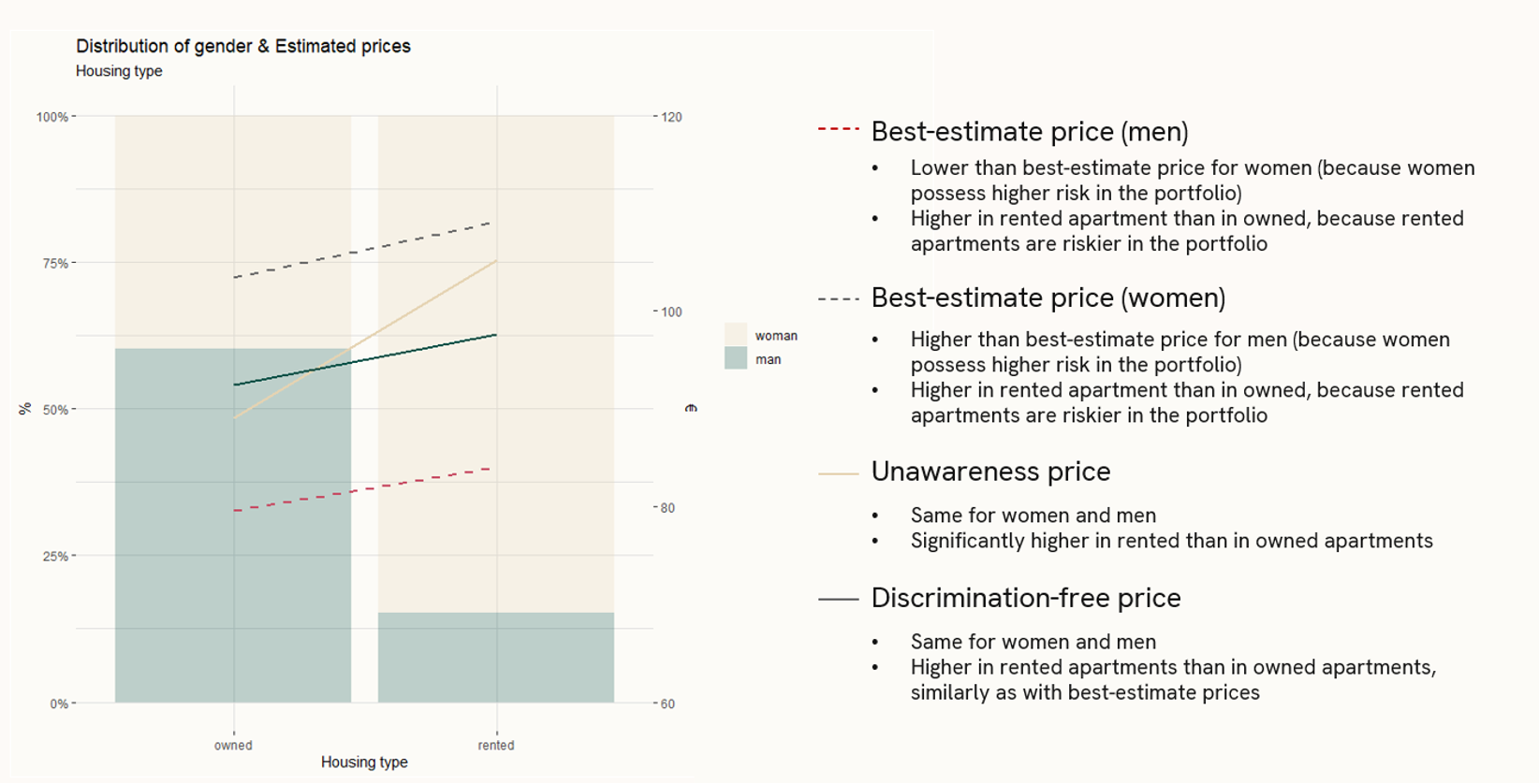
In Figure 2, the best-estimate prices for women (grey dotted line) are higher than for men (red dotted line), since women possess greater risk in the example. In addition, the prices are higher in rented apartments than in owned apartments, again because rented apartments are riskier in the example.
The potential indirect discrimination can be observed by looking at the unawareness prices (beige line). Since gender is not used in estimating the unawareness price, it is the same for men and women. However, what should be noted is that it differentiates between owned and rented apartments more than the best estimate-prices, which is an indication of possible indirect discrimination.
As can be seen in Figure 2, the gender distribution differs between rented and owned apartments; the policyholders in rented apartments are more likely to be women. Since gender has an impact to the housing type, and women possess higher risk in the example, the implicit impact of gender is included in the unawareness prices, even though gender is not explicitly used in the models.
The discrimination-free prices (green line) eliminate this indirect impact, and it differentiates between rented and owned apartments roughly similarly as the best-estimate prices (that is, the price difference between rented and owned apartments is explained purely by the risks associated to different housing types).
Although the example above is simple, it shows that indirect discrimination might occur even though direct discrimination is eliminated. In real-world situations, the models are increasingly complex which elevates the likelihood of the presence of indirect discrimination.
What are the challenges for insurers?
The procedure for removing indirect discrimination in statistical models is conceptually relatively straightforward. However, it is not without challenges.

Ensuring legal compliance with regards to differential pricing practices may become a relatively large challenge going forward for the entire non-life insurance industry in the EU. Based on EIOPA’s recent statement, several expectations for the industry are mentioned with regards to differential pricing practices. Since EIOPA specifically mentions that reasonable efforts must be made to ensure that “the datasets used for differential pricing practices and the outcomes of complex algorithms and technologies are free of bias”, this implies an expectation of datasets and pricing models that are discrimination-free.
Analyzing bias in datasets could be a challenge from a data management perspective. A significant implication is that discrimination-free pricing in general requires the collection of discriminatory characteristics from policyholders. Collecting this data could be practically infeasible since it could potentially be sensitive information that policyholders do not want to disclose.
Furthermore, actively asking for sensitive information could potentially raise ethical concerns and could lead to a situation of increased reputational risk for a company. Especially if it is not entirely clear for the customer why this information is collected. In addition, the procedure might involve some operational challenges. Although the statistical approach is not conceptually difficult, it may become difficult in practice, especially when using larger datasets and more complex model structures. In other words, performing the above-described statistical maneuvers could be expensive. It is also uncertain whether government regulators would have the technical know-how to guarantee that this process was carried out correctly and wasn’t manipulated for illegal purposes.
Next steps and conclusion
The area of differential pricing practices has received increased attention from EIOPA and other supervisory authorities, as well as in academia. For insurance companies as well as insurance distributors, it will be particularly important to follow local supervisory authorities’ response to EIOPA’s supervisory statement on differential pricing practices in non-life insurance lines of business. This is expected to engage several functions within the insurance companies, and not only – as tradition often has it – the product and pricing teams. It is specifically expected to see higher degree of involvement and collaboration between the actuarial, compliance and risk management functions, to ensure that appropriate POG measurers are in place and that customers are treated fairly and offered fair premiums for the insurance products. It is likely that companies need to decide on fairness criteria for their pricing models and the data underlying them – and to understand its impact on strategic goals.
Furthermore, companies may benefit from:
- Conducting internal reviews of e.g., POG processes, pricing models and strategies
- Collect and analyze data,
- Consult with legal and regulatory experts,
- Ensuring that the internal compliance and risk function, in addition to the pricing team are involved from an early stage of e.g., product approval processes.
Appendix
Appendix 1 – Technical details of discrimination-free prices
Appendix 2 – Illustrative example
To find out more on differential pricing and learn how FCG can help you with pricing or other actuarial services, please contact:




[1] Lindholm, M., Richman, R., Tsanakas, A., & Wüthrich, M. (2022). DISCRIMINATION-FREE INSURANCE PRICING. ASTIN Bulletin: The Journal of the IAA, 52(1), 55-89. doi:10.1017/asb.2021.23

